LU Decomposition Calculator: A Simple Guide for Math Enthusiasts

February 28, 2025 Admin

Introduction

Ever found yourself tangled in a mess of simultaneous equations, wondering if there’s an easier way to solve them? Well, you’re in luck! The LU decomposition calculator is a powerful tool that helps break down complex matrix equations into simpler, more manageable forms. Whether you’re a student, engineer, or math enthusiast, understanding LU decomposition can make your calculations faster and more efficient.

In this blog post, we’ll explore what LU decomposition is, how it works, and how an LU decomposition calculator can save you time. Plus, we’ll answer some common questions to help you get the most out of this mathematical technique.

What is LU Decomposition?

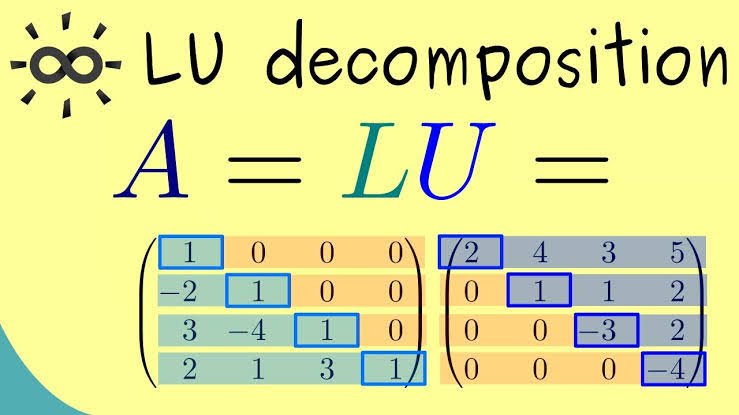
LU decomposition, short for Lower-Upper decomposition, is a method used to factorize a square matrix into two triangular matrices:

L (Lower triangular matrix): A matrix where all elements above the diagonal are zero.
U (Upper triangular matrix): A matrix where all elements below the diagonal are zero.

Mathematically, if AAA is a square matrix, then LU decomposition expresses it as:A=LUA = LUA=LU

where:

LLL has ones on its diagonal and zeros above the diagonal.
UUU has all zeros below the diagonal.

This decomposition makes solving systems of linear equations much easier and faster compared to traditional row-reduction methods.

Why Use an LU Decomposition Calculator?

Solving matrices by hand can be time-consuming and prone to errors. That’s where an LU decomposition calculator comes in handy. Here’s why you should use one:

✅ Saves Time – No need to manually compute lower and upper matrices.
✅ Error-Free Calculations – Reduces the risk of mistakes in calculations.
✅ Handles Large Matrices – Useful for big datasets that would be hard to solve by hand.
✅ Easy to Use – Just input your matrix, and the calculator does the rest.

How Does an LU Decomposition Calculator Work?

Most LU decomposition calculators work in a step-by-step manner:

Input the Matrix – Enter the square matrix (e.g., 3×3, 4×4, etc.).
Perform Decomposition – The calculator uses Gaussian elimination to break the matrix into L and U.
Display Results – The output shows the L and U matrices so you can use them to solve equations.

Some advanced calculators also allow you to enter multiple equations and will automatically solve them using LU decomposition.

How to Use an LU Decomposition Calculator?

Let’s go through an example step by step:

Example:

Suppose we have the following 3×3 matrix:A=[2314736185]A = \begin{bmatrix} 2 & 3 & 1 \\ 4 & 7 & 3 \\ 6 & 18 & 5 \end{bmatrix}A=2463718135

Steps to Solve Using LU Decomposition Calculator:

1️⃣ Enter Matrix A into the calculator.
2️⃣ Press “Calculate” – The calculator applies LU factorization.
3️⃣ Get the result:

Lower Triangular Matrix (L):L=[100210341]L = \begin{bmatrix} 1 & 0 & 0 \\ 2 & 1 & 0 \\ 3 & 4 & 1 \end{bmatrix}L=123014001
Upper Triangular Matrix (U):U=[231011002]U = \begin{bmatrix} 2 & 3 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 2 \end{bmatrix}U=200310112

Now, you can use forward and backward substitution to solve for unknowns in a system of equations.

Applications of LU Decomposition

LU decomposition is widely used in various fields, including:

🔹 Engineering & Physics – Solving structural and electrical circuit equations.
🔹 Computer Science – Used in numerical algorithms for machine learning and AI.
🔹 Finance & Economics – Helps in risk modeling and economic forecasting.
🔹 Data Science – Optimizes large-scale computations in analytics.

Whether you’re working on scientific computing or just trying to speed up homework problems, an LU decomposition calculator can be your best friend.

Common Mistakes and How to Avoid Them

Even though LU decomposition is a powerful technique, some pitfalls can lead to incorrect results. Here are some common mistakes:

❌ Using Non-Square Matrices – LU decomposition only works for square matrices (e.g., 3×3, 4×4).
❌ Ignoring Singular Matrices – If a matrix has a zero determinant, LU decomposition may not be possible.
❌ Incorrect Pivoting – Some matrices require partial pivoting to avoid division by zero errors.

A good LU decomposition calculator automatically handles these issues, so you don’t have to worry about them.

Conclusion

lu decomposition calculator is an essential technique in mathematics and engineering, allowing for faster and more efficient solutions to linear equations. Instead of doing long calculations by hand, an LU decomposition calculator makes the process quick and error-free.

So next time you encounter a matrix problem, let an LU decomposition calculator do the heavy lifting for you! 🚀

FAQs (Frequently Asked Questions)

1. Can LU decomposition be used for non-square matrices?

No, LU decomposition only works for square matrices (e.g., 2×2, 3×3, etc.). For non-square matrices, other methods like QR decomposition are used.

2. What happens if LU decomposition fails?

LU decomposition may fail if the matrix is singular (i.e., determinant = 0). In such cases, you might need to apply pivoting or use other techniques like Cholesky decomposition (for positive definite matrices).

3. Is LU decomposition the same as Gaussian elimination?

Not exactly. LU decomposition is based on Gaussian elimination, but instead of solving the system directly, it splits the matrix into L and U for easier calculations.

4. Can LU decomposition be used for real-world applications?

Yes! It is widely used in engineering, physics, computer science, and finance for solving complex mathematical problems efficiently.

5. Where can I find a reliable LU decomposition calculator?

You can find online LU decomposition calculators on various math solver websites or use built-in functions in Python (NumPy), MATLAB, and R for matrix factorization.